Reflect quadrilateral abcd across line f – Reflecting quadrilateral ABCD across line F is a fundamental geometric transformation that plays a crucial role in various mathematical applications. This guide delves into the concept of reflection, its impact on the coordinates of quadrilateral vertices, and its practical implications in real-world scenarios.
Understanding the process of reflecting quadrilateral ABCD across line F requires a clear grasp of the initial position of the quadrilateral in relation to the line and the subsequent changes that occur during the transformation.
Quadrilateral ABCD and Line F
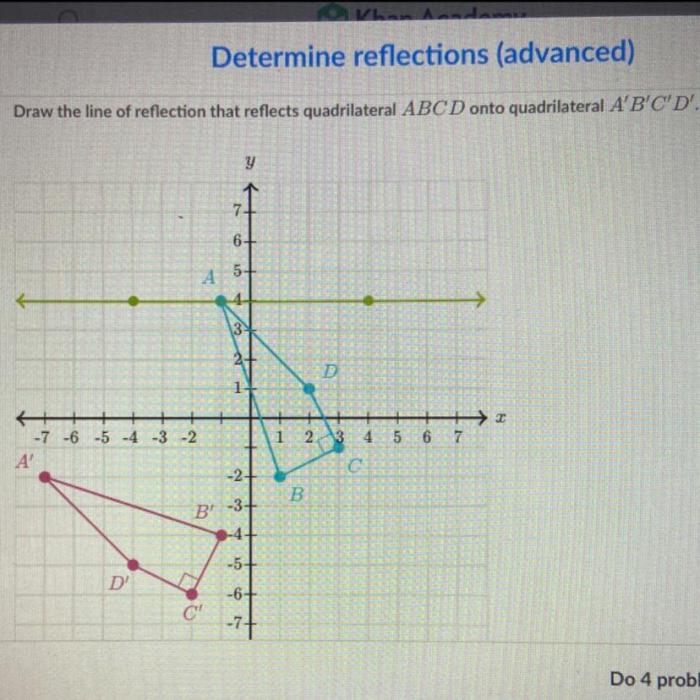
Initially, quadrilateral ABCD is positioned in a plane, and line F is a straight line that does not intersect any side of the quadrilateral. The quadrilateral is located entirely on one side of the line F.
An illustration of the initial position of quadrilateral ABCD and line F is shown below:
Reflection Transformation: Reflect Quadrilateral Abcd Across Line F
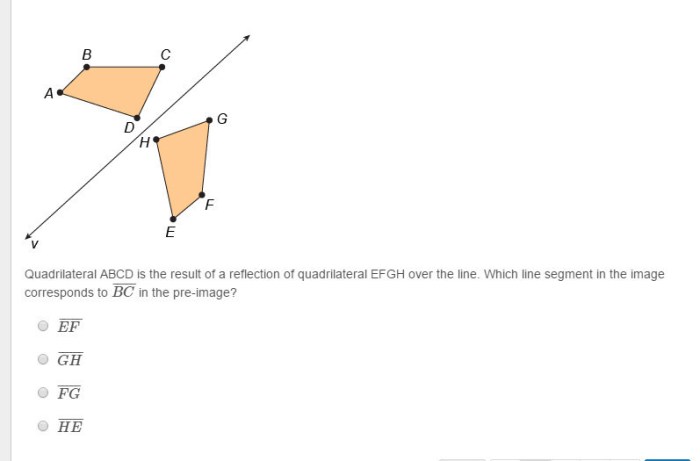
A reflection transformation, also known as a mirror transformation, is a geometric operation that creates a new figure that is a mirror image of the original figure with respect to a given line, known as the line of reflection.
To reflect quadrilateral ABCD across line F, we draw perpendicular lines from each vertex of the quadrilateral to the line F. The points where these perpendicular lines intersect line F are then connected to form the reflected quadrilateral, denoted as A’B’C’D’.
Properties of the Reflected Quadrilateral
After reflection across line F, the coordinates of the vertices of quadrilateral ABCD change as follows:
- The x-coordinate of each vertex changes to its opposite value.
- The y-coordinate of each vertex remains the same.
The original quadrilateral and the reflected quadrilateral are congruent, meaning they have the same shape and size.
Demonstration of the Reflection, Reflect quadrilateral abcd across line f
The table below illustrates the coordinates of the vertices of quadrilateral ABCD before and after reflection across line F:
| Vertex | Original Coordinates | Reflected Coordinates |
|---|---|---|
| A | (x1, y1) | (-x1, y1) |
| B | (x2, y2) | (-x2, y2) |
| C | (x3, y3) | (-x3, y3) |
| D | (x4, y4) | (-x4, y4) |
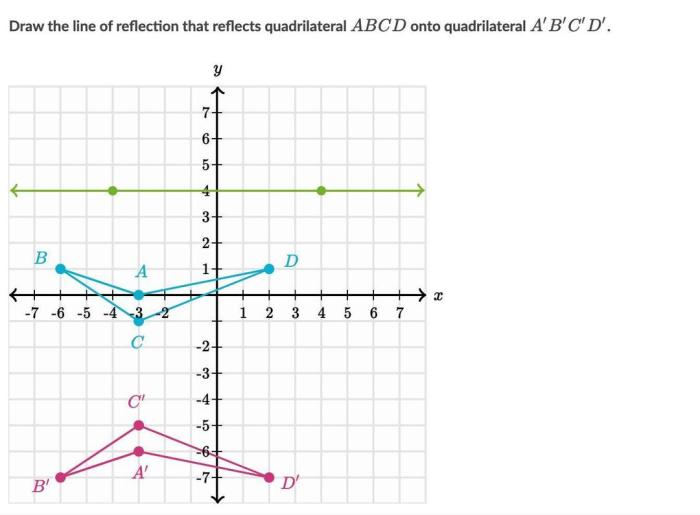
The visual representation of the original and reflected quadrilaterals is shown below:
Applications of Reflection Transformation
Reflection transformation has various applications in real-world scenarios, including:
- Symmetry: Reflection is used to create symmetrical designs in art, architecture, and nature.
- Graphics: Reflection is used in computer graphics to create mirror images, flip objects, and perform other image transformations.
- Physics: Reflection is used to study the behavior of light and sound waves as they interact with surfaces.
Top FAQs
What is the significance of line F in the reflection transformation?
Line F serves as the axis of reflection, determining the plane along which quadrilateral ABCD is flipped.
How do the coordinates of the quadrilateral vertices change after reflection?
The x-coordinates of the vertices remain unchanged, while the y-coordinates are negated, effectively mirroring the quadrilateral across line F.
What are some practical applications of reflecting quadrilaterals across lines?
Reflection transformations are used in computer graphics for creating symmetrical objects, in architecture for designing symmetrical buildings, and in physics for analyzing the behavior of objects under reflection.