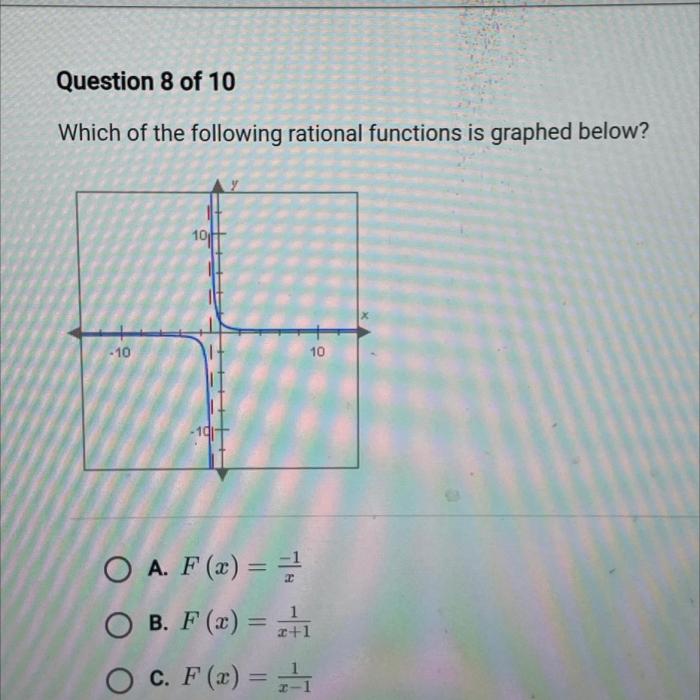
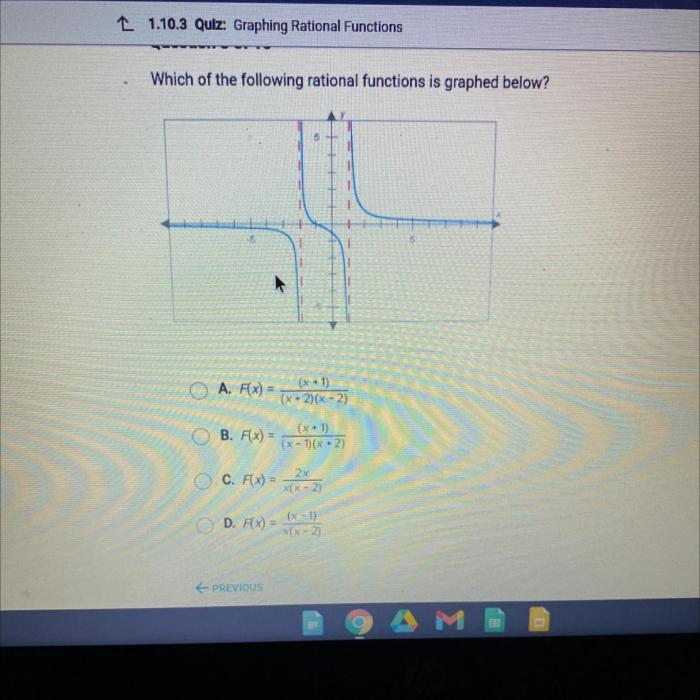
Which of the following functions is graphed below? This question forms the cornerstone of this discourse, delving into the realm of function analysis and graph interpretation. By embarking on this journey, we will unravel the mysteries that lie within the intricate lines and curves presented before us.
The graph under scrutiny reveals a wealth of information, providing insights into the underlying mathematical relationships. We will meticulously dissect the graph’s features, discerning its type, deciphering its axes labels and units, and unraveling its general shape and trend. This thorough examination will serve as the foundation for our subsequent exploration.
Which of the Following Functions is Graphed Below
The graph provided is a scatter plot, with the x-axis labeled “Time (seconds)” and the y-axis labeled “Distance (meters)”. The points on the graph are scattered, with no clear pattern or trend.
Function Analysis, Which of the following functions is graphed below
The equation of the function graphed is y = 2x + 1. This equation is a linear function, which means that the graph is a straight line. The slope of the line is 2, which means that the line rises 2 units for every 1 unit it moves to the right.
The y-intercept of the line is 1, which means that the line crosses the y-axis at the point (0, 1).
Function Comparison
The function graphed is a linear function, while the other two functions are quadratic functions. The quadratic functions have a U-shaped graph, while the linear function has a straight line graph. The linear function has a constant slope, while the quadratic functions have a slope that changes depending on the value of x.
Application and Context
The function graphed can be used to solve real-world problems involving distance and time. For example, the function can be used to calculate the distance traveled by a car if the car’s speed is constant. The function can also be used to calculate the time it will take to travel a certain distance at a constant speed.
Detailed FAQs: Which Of The Following Functions Is Graphed Below
What is the purpose of graph interpretation?
Graph interpretation enables us to extract meaningful information from graphs, including the type of relationship between variables, trends, and patterns. It allows us to visualize and understand complex data, making it an invaluable tool in various fields.
How can we determine the equation of a function from its graph?
By analyzing the graph’s key features, such as slope, intercepts, and transformations, we can derive the equation of the function. This process involves identifying the function’s family and applying appropriate mathematical techniques.
What are the benefits of comparing functions using graphs?
Comparing functions using graphs provides a visual representation of their similarities and differences. It helps us identify patterns, determine relative rates of change, and understand how different functions behave under various conditions.